Stealth Feeless Transactions and Powerful Spam Prevention

January 24, 2022

This blog post describes Stealth feeless transactions in detail, and represents the first part of a full description of the Stealth blockchain protocol. In some ways it is a draft, but in practicality is intended to be a living, evolving document that will find hosting somewhere on stealth.org or our code repositories. I will add several more contributions over the coming months to complete the description of the Stealth cryptocurrency.

 

Introduction to Feeless Transactions

Our most recent wallet release is StealthSend Desktop, the desktop version of our StealthSend wallet for the XST cryptocurrency. Previously available only as a mobile wallet, StealthSend Desktop offers all the same features as the mobile version, plus optional feeless transactions.

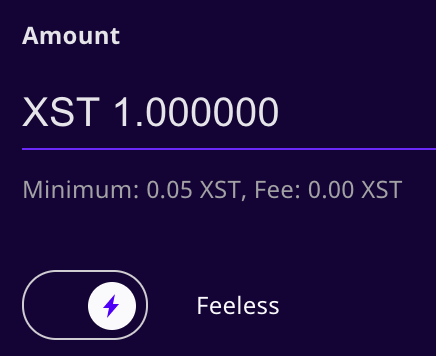
A user who wants to pay fees needs only to slide the switch to the left, as shown in the following figure:

Disabling the feeless option adds a minimum 0.01 XST to the cost of the transaction, indicated in the dialog (not shown here). The tradeoff is that opting into fees speeds up generation of the transaction by about 1 second on average. In a feeless transaction, that second is used by the sender’s computer to solve a cryptographic puzzle that is similar to Bitcoin mining.

However, instead of mining cryptocurrency, the sender’s computer mines the right to send a single transaction without the need for a fee. This computing effort is called “feework”. Feework is also unlike Bitcoin mining in that feework requires negligible energy and hence has negligible environmental impact.

 

 

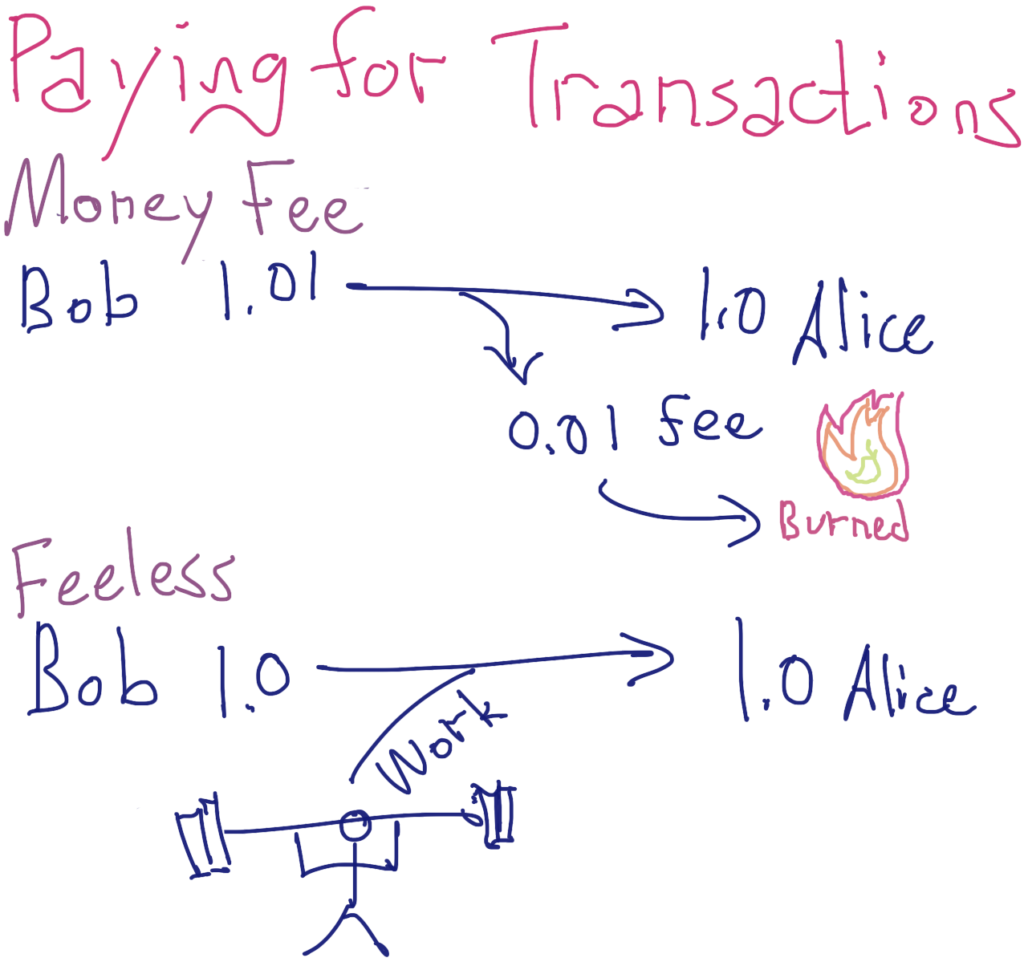
A cryptographic proof of this feework is attached to the transaction as a sort of digital coupon. This coupon is highly specific not only to the transaction, but the precise moment in time the coupon was created. This temporal specificity lies at the heart of Stealth’s powerful approach to fighting spam.

— — — — — — —

 

Benefits of Feeless Transactions

While Stealth’s standard fee of 0.01 XST is much less than one cent, feeless transactions still represent a significant usability improvement over money fee transactions.

First, feeless transactions facilitate so-called microtransactions that can be valued at fractions of a cent. As I write this post, the smallest amount of XST that a user may send in a transaction is valued at about $0.00025 (USD), or 0.025 cents. If this type of transaction were sent using a money fee, then, at current rates, the transaction would cost as much as the amount sent for XST. In other words, the smallest transaction would require a fee of 100%. Bitcoin of course would be far worse and is entirely unusable for microtransactions. Sending the smallest amount of Bitcoin would cost nearly $2 at the time of writing.

Microtransactions can serve many purposes, such as pre-paying for streaming or electrical charging services by the minute. Another use is as a voting system where each “ballot” transfers minimum transaction size (currently $0.0005). With feeless transactions, the value of these ballots can be fully reclaimed to the extent that the balloters exercise their votes.

Second, feeless transactions relieve a morass of accounting issues. Perhaps the biggest relief is that one never needs to check one’s balance or the cost of transaction fees before committing to a transaction. Those who have used Ethereum for defi (“decentralized finance”) or NFTs (non-fungible tokens) in the last couple of years know well the hazards of insufficient fees. The greatest risk comes from under-estimating fees then committing to a transaction that then runs out of “gas” (fee money).

Each Ethereum transaction is a spin of the roulette wheel, where expensive gas (ETH) is wagered on a successful transaction. In some cases, these lost fees are thousands of US dollars for a single transaction.

Another accounting relief comes from taxes, where each cryptocurrency fee is actually taxable. It goes without saying that tracking these fees quickly becomes impractical, making the strictly legal use of any money fee cryptocurrency nearly impossible in many jurisdictions.

Feeless transactions are supported by only a handful of cryptocurrencies, the most notable of which are Stealth (XST), Nano (XNO), Hive (HIVE), IOTA, and derivatives thereof (e.g. Banano, Eos). Few cryptocurrencies support feeless transactions because of the difficulty to prevent spam, where spammers create volumes of low-value transactions in an effort to overwhelm the network. Heavy spam can cause the network to lose synchronization, lose consensus, and inundate resources like CPU power and disk storage.

— — — — — — —

 

Stealth’s Lead Feeless Competitor: Nano

Of Stealth’s feeless competitors, Nano has the most efficient design as well as the most powerful approach to fighting spam. I will compare, in detail, Nano’s feeless technology with that of Stealth to show how Stealth fights spam with even greater efficacy than Nano.

Please make note that this comparison is not an indictment of the Nano protocol. On the contrary, Nano is considered a leader among feeless cryptocurrencies because it has a robust protocol and is therefore the most logical cryptocurrency to compare with Stealth.

Early in 2021, Nano suffered a months-long spam attack that peaked at nearly 5M transactions per day and prompted significant changes to Nano’s protocol to fight spam. Prior to that attack, Stealth’s feeless transactions were already functional on testnet, the release of which was accompanied by a blog post that doubled as the Stealth feeless transaction whitepaper. Some of Nano’s eventual anti-spam measures bore resemblance to those already implemented and functional on the Stealth testnet. But at its core, Nano’s approach to fighting spam is unique and fundamentally different from Stealth’s approach.

— — — — — — —

 

Nano’s Spam Fighting Technology

In Nano’s consensus mechanism, delegate accounts vote on individual transactions. If a majority of network voting weight approves a transaction, it gets confirmed. In Nano’s new anti-spam protocol, Nano sorts all unconfirmed transactions into 129 different buckets, where each bucket represents a range of account balances. For example, bucket 100 serves accounts with balances ranging from about 0.6338 XNO to about 1.2675 XNO.

 

 

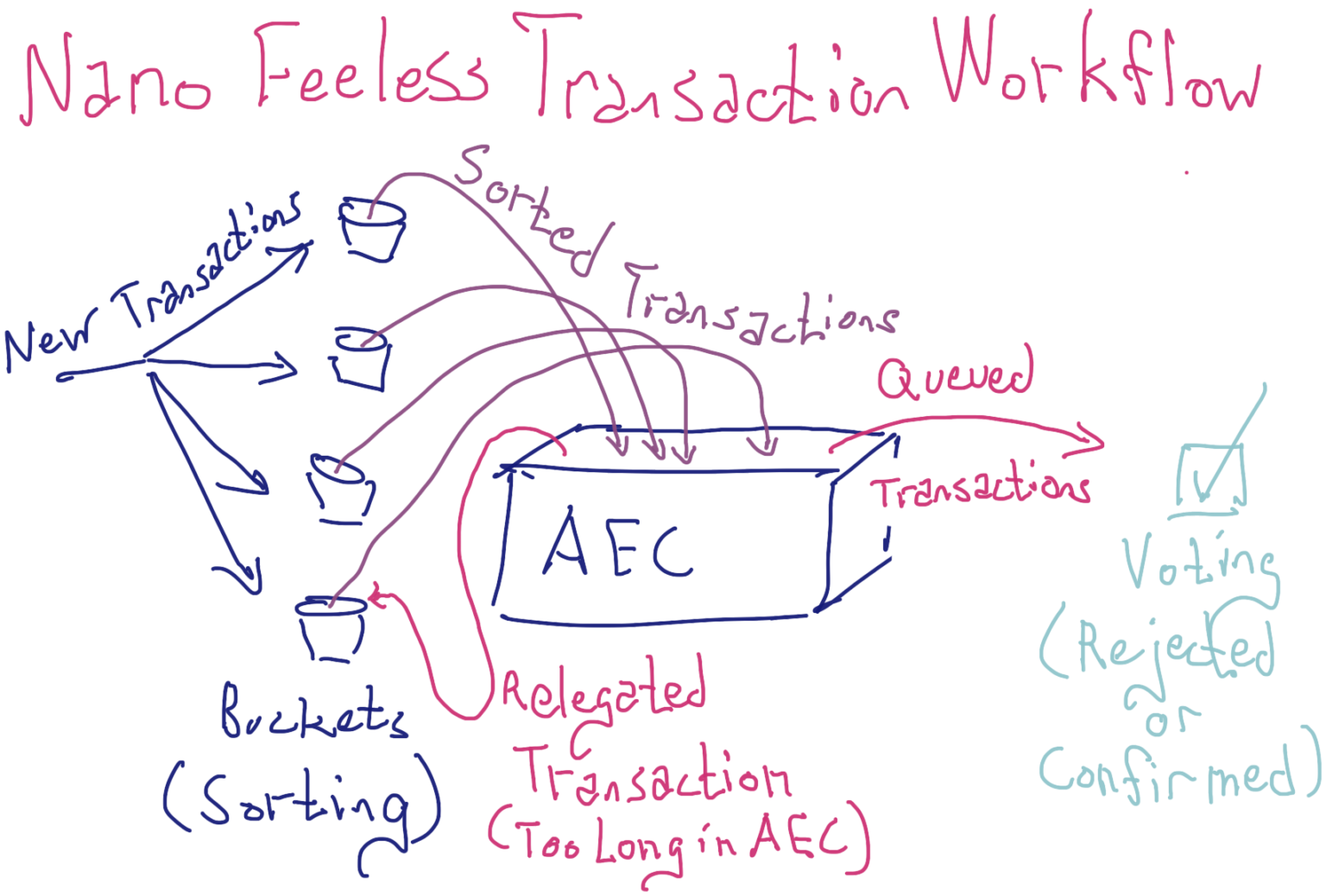
Unconfirmed transactions in a bucket are then sorted by how recently the account was used, with less recently used accounts having priority. The rationale for this priority system is that spammers will use their accounts very frequently to send spam, so they will be more recently used than accounts conducting more purposeful transactions. From these buckets, about 50,000 transactions are selected as candidates for voting. This pool of transactions is called the “Active Election Container” (AEC). If a transaction is not confirmed from the AEC within 5 minutes, it is removed from the AEC and put back in its bucket. This relegation from the AEC helps a node flip through transactions until it finds those that are being actively voted, effectively allowing the node to “synchronize” with the rest of the network and contribute productively to Nano’s security.

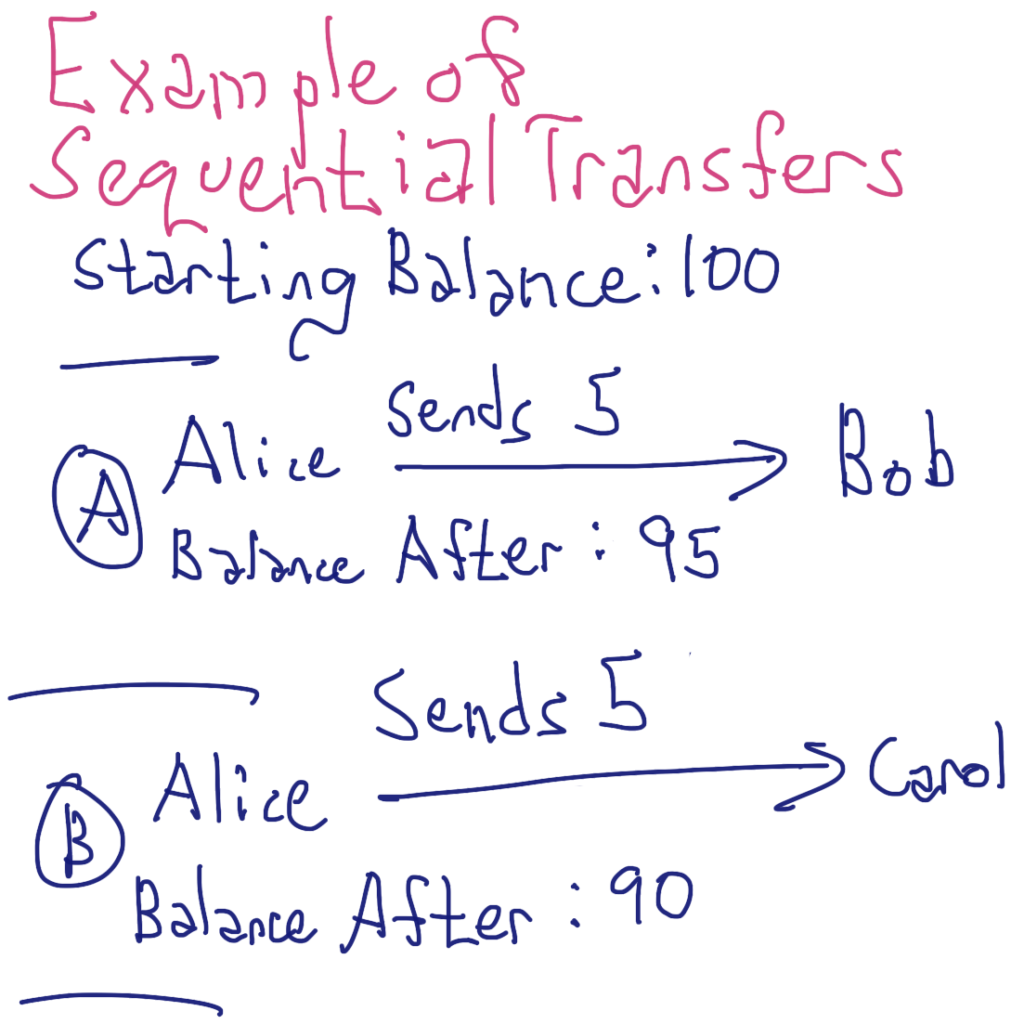
A critical part of Nano’s anti-spam technology is that new transactions are considered invalid if they do not have confirmed predecessors. For example, starting with a balance of 100 XNO, if Alice sends 5 XNO to Bob in Transaction A then Alice sends 5 XNO to Carol in Transaction B, the network drops Transaction B for voting if Transaction A has yet to be confirmed. This requirement effectively limits the rate of spam proportional to the speed of voting.

 

 

Nano’s anti-spam improvements neutralized the most vicious spam attack in cryptocurrency history, and allowed the entire Nano network to begin functioning normally within a couple of weeks of implementation. However, Nano’s approach does have some theoretical vulnerabilities and significant utility tradeoffs.

One critical issue is that active accounts are not distributed evenly within Nano’s bucket structure. Another way to understand this disparity is that there are many more active Nano accounts with balances around 5 XNO than there are with balances around 0.00001 XNO, even though these two buckets will get the same prioritization for inclusion into the AEC. Thus, a spammer can gain an advantage over legitimate accounts by spamming dozens of small-balance buckets through which legitimate accounts seldom send. For example, 87 buckets are reserved for account balances that are less than one ten-thousandth of an XNO (0.0001 XNO). Having 1000 accounts in each of these buckets (87,000 accounts in total) would only require 0.2 XNO, worth about $0.40 at the time of writing.

A second problem with Nano’s anti-spam measures is that spammers can continue to add transactions to buckets indefinitely. If spammers fill buckets faster than validators can empty them with confirmations, then unprocessed spam transactions will require a steady growth of system memory or disk storage. The reason is that Nano transactions have no expiration, so they can persist forever. Even if an unconfirmed spam transaction is cleared from a node’s buckets for persisting too long in memory (or having an unconfirmed predecessor), the transaction can simply be resubmitted to the network without any additional work from the spammer. Worse yet, a spammer could spend months preparing tens of millions of transactions to spam the Nano network all at once.

— — — — — — —

 

Nano’s Asynchrony is Double Edged

The root of this inability to expire transactions is that the Nano consensus protocol has no concept of network time, owing to the asynchronous nature of its so-called “block lattice” distributed data structure. To understand Nano’s asynchrony, it is necessary to understand its block lattice.

In Nano’s block lattice, each transaction is a “block” and each account (or address) has its own blockchain. Nano account blockchains are similar to other types of blockchains in that they form proper chains: each block has one and only one immediate predecessor and one and only one immediate successor, with the exception of the first block for the account, of course, which has no predecessor. With millions of accounts, Nano’s block lattice has millions of blockchains.

The utility of a block lattice arises from how Nano treats value transfers. Consider two accounts, Alice and Bob, where Alice starts with a balance of 100 XNO and transfers 1 XNO to Bob in Block A (remember that each transaction is a “block” in Nano). To execute this send, Alice appends Block A to her blockchain deducting 1 XNO from her balance. This block authorizes Bob to later append Block B to his blockchain that adds 1 XNO to his balance, changing Bob’s balance from 10 XNO to 11 XNO. Block B, in which Bob adds this 1 XNO to his balance, references Block A where Alice sent him 1 XNO.

 

 

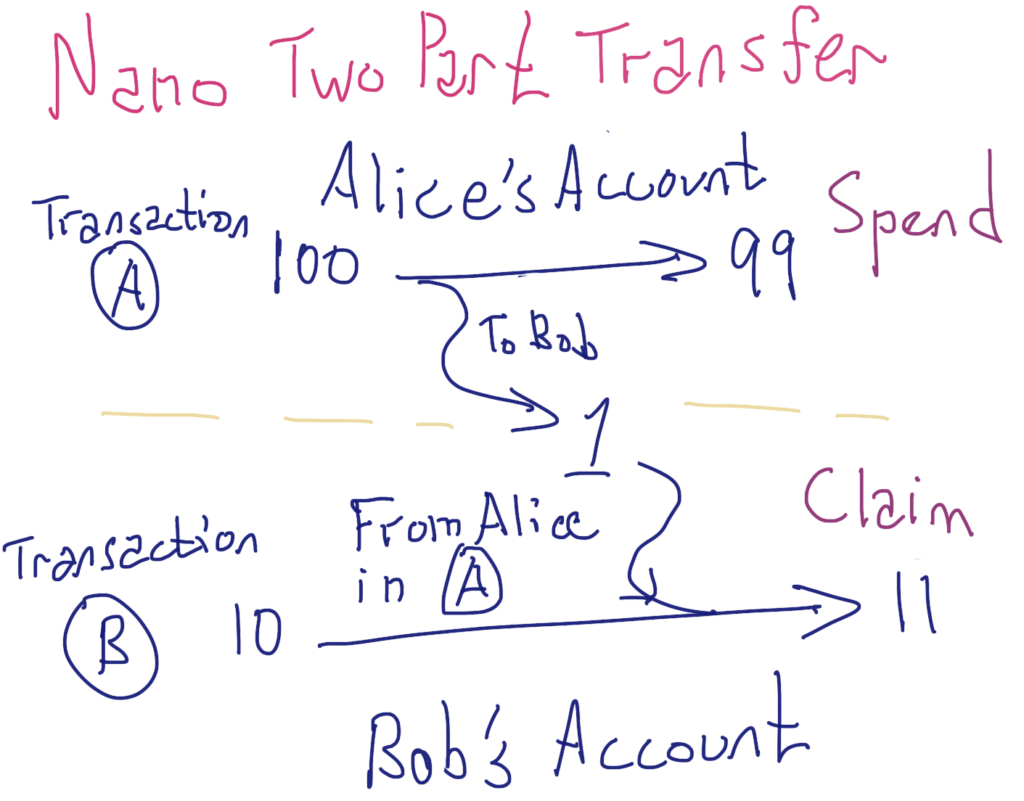
From this example, it is clear that each transfer requires two blocks: one block to deduct from the sender’s account (Block A in this example) and one to add to the recipient’s account (Block B in this example).

Although this system may at first seem unnecessarily complicated, it addresses a number of problems inherent to distributed cash. First, it is easy to tell if an account attempts to spend money it doesn’t have. Since the blocks of a particular account form a proper chain, it is trivial to calculate an account’s balance at any given moment by summing the balance changes over all the blocks of the account’s blockchain, in order. Second, validators don’t waste any computational overhead attempting to order transactions within blocks of transactions. Like balance changes, transactional ordering is completely specified by account owners, subject to the rule that an account may never have a negative balance. Third, the account-based system means that network nodes do not have to track unspent money, only account balances. Fourth, because sending is separated from receiving, all transactions can progress asynchronously relative to each other.

This type of asynchrony is efficient because it allows nearly instantaneous transactions and a pleasing user experience. For example, to create a new transaction, Bob does not have to wait for any other transactions to confirm outside of his most recent transaction.

Importantly, Nano’s approach to fighting spam necessarily sacrifices some of the utility of its asynchronous protocol because accounts are only allowed to submit one unconfirmed transaction at a time. For example, if Alice wants to send both Bob and Carol 1 XNO each, one of these transactions will be invalid until the other is confirmed. Utility is lost by accounts that may have a large number of payees. Each payee must be paid in a separate transaction, and each transaction must await its predecessor’s confirmation.

The tradeoff for the efficiency afforded by asynchrony is that it is impossible to order two transactions that do not share a common history. For example, imagine (A) Alice sends 1 XNO to Bob, (B) then 1 XNO to Carol. Sometime after Transaction A, (C) Bob sends 1 XNO to Diane and (D) Carol sends 1 XNO to Edgar. This scenario is depicted in the following figure:

 

 

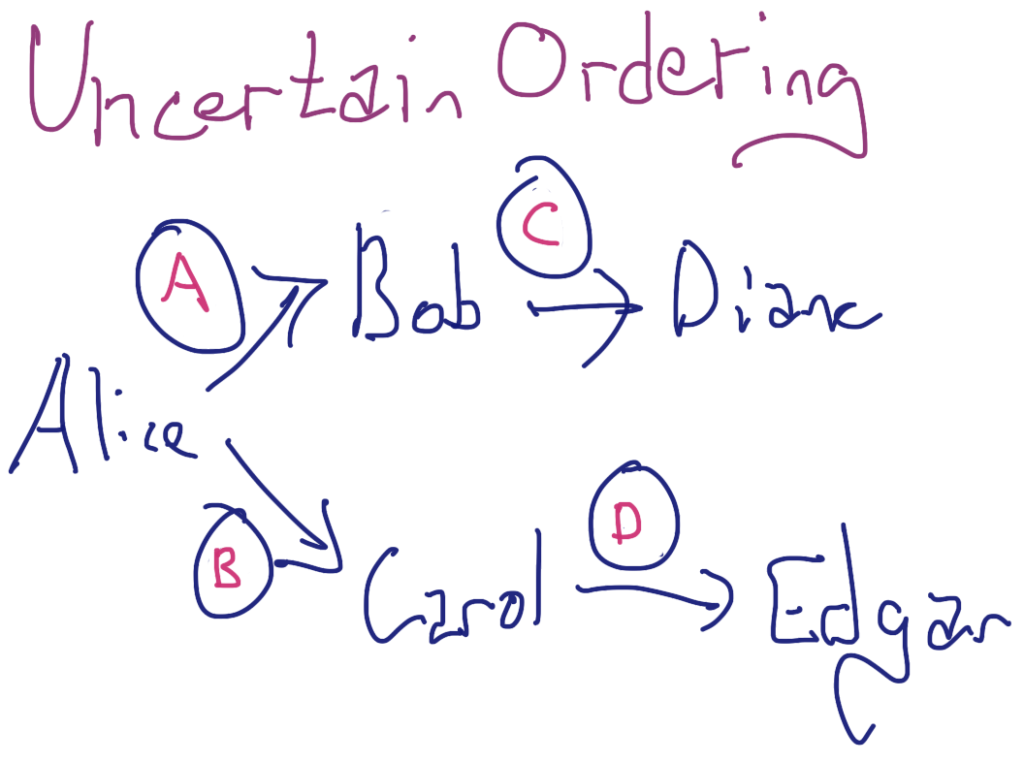
Asynchrony means that it is impossible to know whether Transaction C happened temporally before Transaction D. Although more difficult to see from this example, it is also impossible to know whether Transaction C happened temporally before Transaction B.

For the strict purpose of keeping a valid ledger, this lack of ordering has no consequence. However, a lack of order can have important implications for fighting spam, as it allows the aforementioned exhaustion of resources by flooding the network with transactions.In contrast to Nano, the Stealth blockchain has ordered blocks. Additionally, transactions within these blocks are fully ordered down to the transactional components called “inputs” and “outputs”. As I will describe below, the Stealth feeless protocol makes full use of all this ordering to fight spam in a far more elegant and effective way than any other blockchain protocol. Importantly, not only does the Stealth protocol enable a more pleasing user experience when under attack, but full ordering enables parallel processing of feeless transactions, dramatically increasing Stealth’s scalability.

— — — — — — —

 

Stealth Blockchain Structure

At the highest level, the Stealth blockchain is composed of blocks ordered sequentially, similar to every proper blockchain. Each Stealth block has a single predecessor (except for block 0) and single successor (except for the “highest”, or most recent, block in the chain). Stealth blocks are made of transactions, and the transactions have an explicit ordering within blocks. Stealth differs from Nano in that Stealth blocks can have many transactions, whereas Nano blocks consist of only a single transaction.

Stealth transactions are composed of inputs and outputs. The nomenclature of inputs and outputs is counterintuitive. An input is the money an address sends away, and an output is the money an address receives. The nomenclature makes sense if we consider money flow from the perspective of the blockchain:

 

 

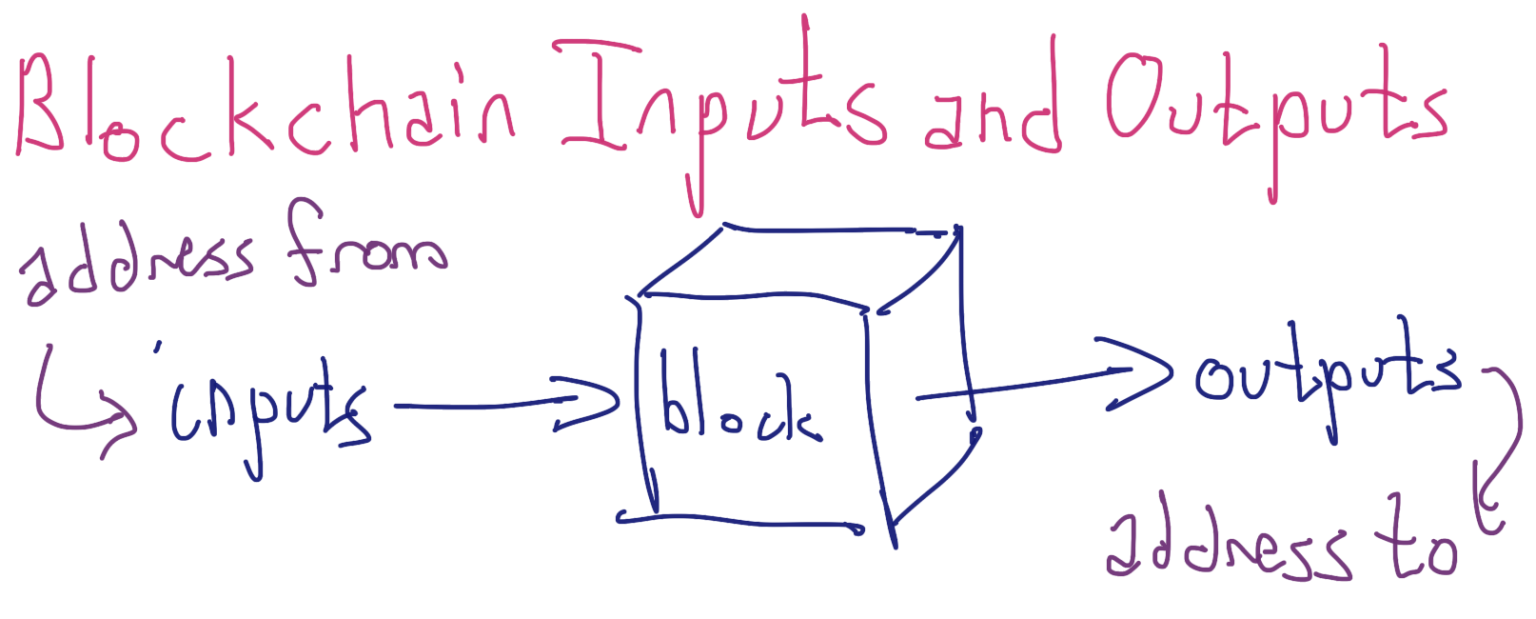
Outputs are known as “unspent” until they are spent and become inputs. The full name of an unspent output is an “unspent transaction output”, or “UTXO” for short. UTXOs are like travelers cheques. Each UTXO has a specific value and can be spent only once. To spend a UTXO, the sender signs it and then redeems it for the amount of the UTXO minus any fees. The value of a UTXO can be redeemed to any combination of recipients, even the sender as change. Blockchains that work this way, like Stealth, Bitcoin, Dogecoin, and Litecoin, are called “UTXO blockchains”.

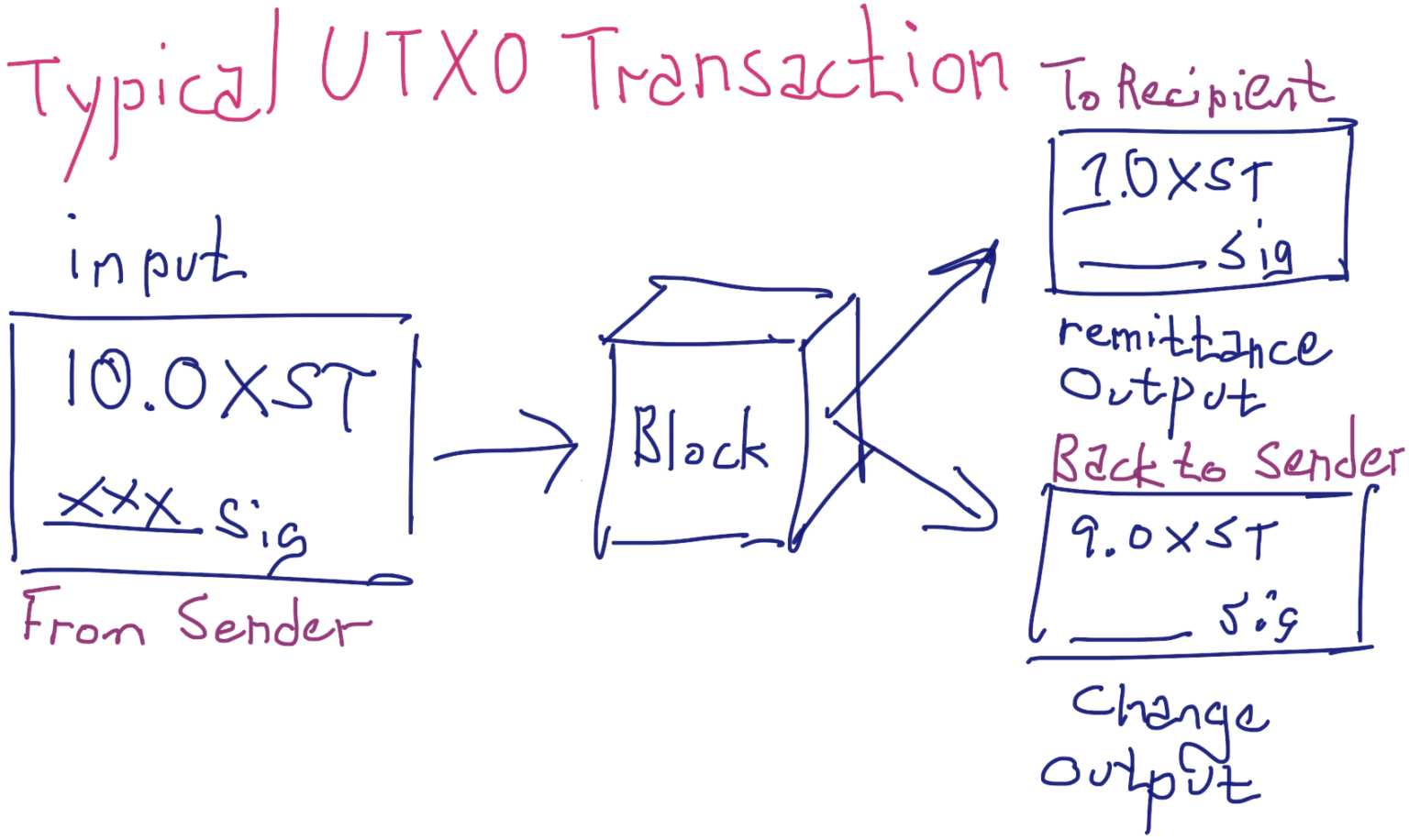
The following figure represents the most common type of UTXO transaction, where one UTXO is spent as an input (the cryptographic signature represented as “XXX”) and remitted to a recipient (here 1.0 XST). Another output (9.0 XST) is sent back to the sender as change. For simplicity, no funds were withheld as fees in this example.

 

 

An important feature of a UTXO blockchain is that a single transaction can combine many inputs and produce many outputs, illustrated schematically in the following figure:

 

 

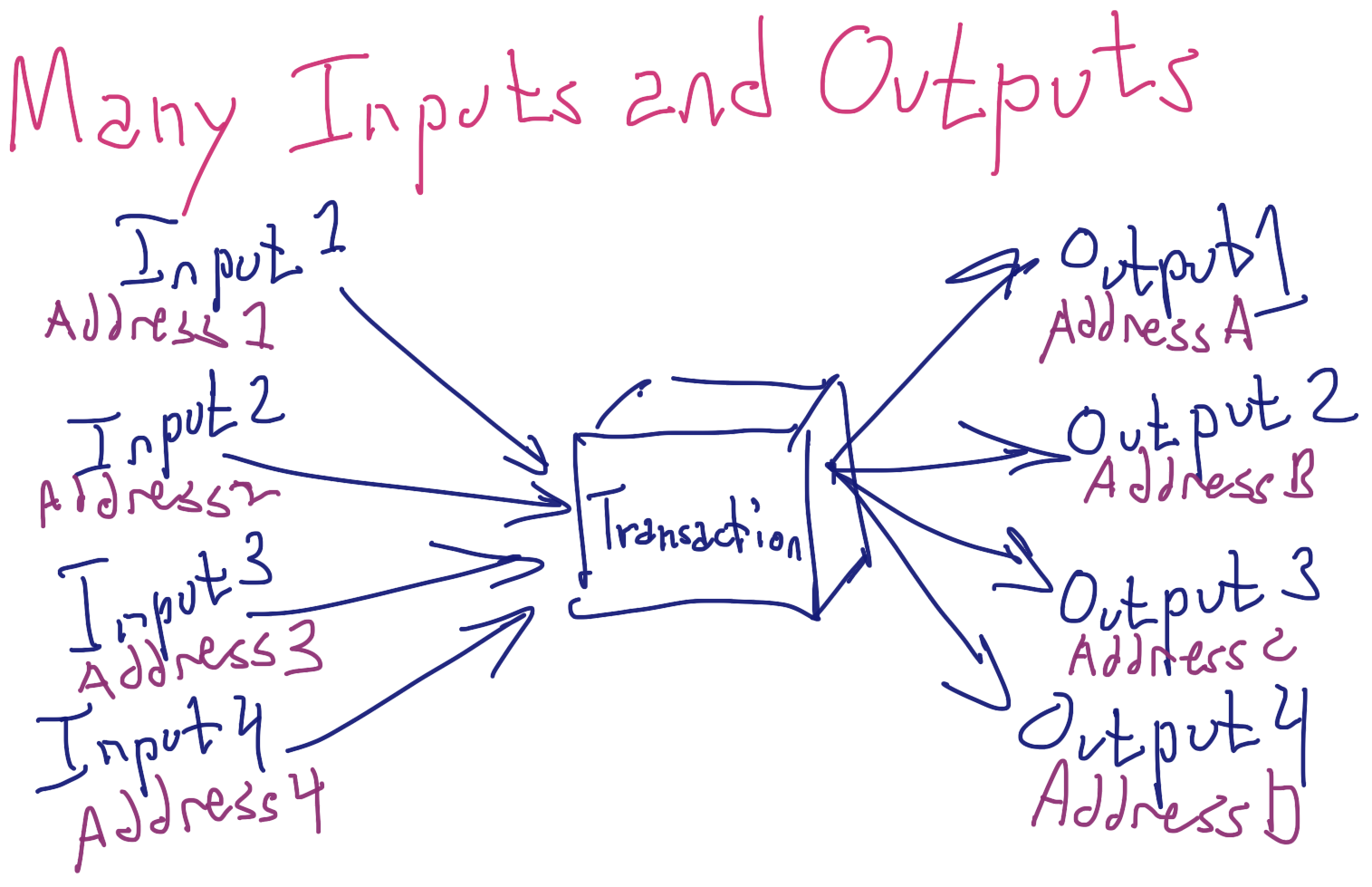
UTXOs to any number of different addresses can serve as inputs for a single transaction, as long as the sender has the credentials needed to sign the inputs. Additionally, any number of different addresses can be paid in a single transaction. This source of concurrency inherent to UTXO blockchains is often overlooked, and represents a mechanism for scaling that is unavailable to Nano.

As components of a transaction, inputs and outputs also have an ordering within the transaction. First, inputs precede outputs. Second, outputs and inputs have an ordering relative to other inputs and outputs, respectively. The ordering of inputs and outputs is only important for the purposes of identifying the type of transaction or for checking whether special transactions are properly formed. For example, Stealth feeless transactions include a special unspendable output that replaces the fee. This so-called “feework” must come after all other outputs.

The position of Stealth’s feework output is not arbitrary. Stored on the blockchain, a Stealth feeless transaction with four inputs and five outputs has the following structure:

 

 

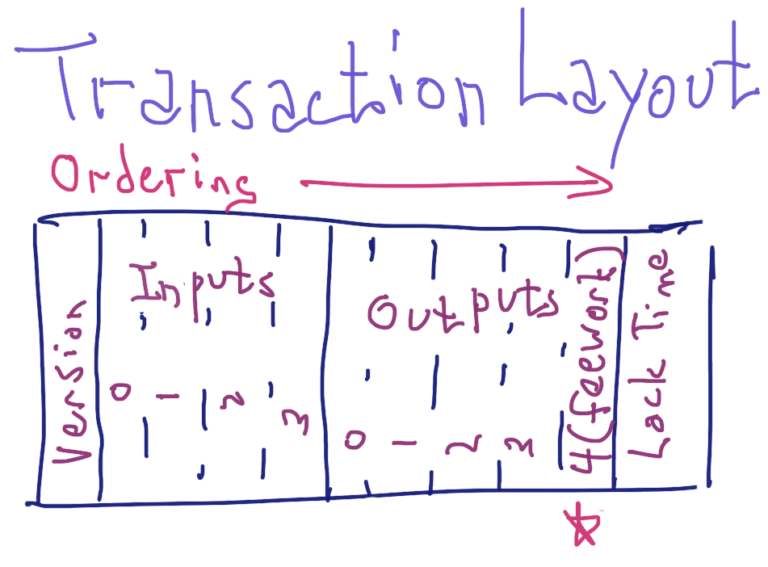
The ordering of information in the blockchain for a transaction begins with the version of the transaction, then the inputs (starting with number 0), the outputs (starting with number 0), and then the transaction lock time. The feework output (i.e. feeless coupon) in this transaction is marked with a star (output number 4).

Although the feework could conceivably be anywhere, its presence at the end of the outputs makes it easy to find. Feeless transactions are therefore not valid if the feework is anywhere but in this last position. This simple rule also invalidates feeless transactions with multiple feework outputs.

— — — — — — —

 

Stealth Feeless Implementation

Stealth’s feeless implementation has two main components: (1) creating feework and (2) validating feework.

To understand both, it is first necessary to understand the concept of a cryptographic hash. Although a drastic oversimplification, a good way to think of a cryptographic hash is that it shuffles and mutates (changes) information (“data”) according to a recipe. For a good cryptographic it is impossible to predict the outcome of the hash without actually following the recipe.

To illustrate this idea, imagine a shuffling where the deck is split into two equal halves, then the cards from each half are interleaved with the other half (the standard procedure most people consider “shuffling”). Then, every card following an ace it changed to a four. Then the deck is split and interleaved. Then every odd club is replaced with the next lower spade. Then many more interleavings and bizarre substitution rules are applied. At the end the deck would bear absolutely no resemblance to its starting state. Cryptographic hashes work in much the same way as this elaborate shuffling.

Cryptographic hash recipes are diverse and very complex. Instead of explaining these recipes (known as “algorithms” in computer science parlance), I will show some examples of hashing data with cryptographic hash functions. A reasonable cryptographic hash function for such examples is known as SHA-1, which is used in Bitcoin address derivation.

Let’s start with some plaintext data: “Stealth rocks!” The SHA-1 of “Stealth rocks!” is a 20 byte number represented as hexadecimal. It is easiest just to think of this number as a 40 character word consisting of all 10 numbers and the letters “a” through “f”:

d08ff9fcaafe5d0af5dd7945fa2460921010849d

This hash can be calculated in python 3 with the following one liner:

import hashlib;print(hashlib.sha1(b"Stealth rocks!").hexdigest())

Notice how the result of the hash bears absolutely no resemblance to the data (“Stealth rocks!”).

Another property of cryptographic hashes is that the slightest change will produce a completely different and unpredictable hash. For example we can change the message to “Stealth socks!”, which changes an “r” to an “s”. This change represents a difference of only one bit, the smallest unit of information. The SHA-1 hash of “Stealth socks!” is:

a21efd5722861683cb7a7d49d33a93143f33a5a8

Notice how this change of a single bit of the data produces a completely different hash with no resemblance to either version of the data or the hash of the unchanged data.

A given cryptographic hash requires a specific amount of computer work to produce, independent of the data. This work is also similar to shuffling a deck of cards, where the shuffling itself requires physical effort. A single shuffle may not require much effort, but shuffling 1,000 decks of cards would quickly get tiring.

Cryptographic hashes are used in proofs. One type of proof is a proof of knowledge, where one publishes the hash of some information secret to the rest of the world. For example, I could publish the SHA-1 hash to a secret phrase:

d70d7180ec6c055b04152619ebd7f1e475082fa7

Given this hash, it would be practically impossible to find a meaningful phrase that produces this SHA-1 hash. Later I could publish the phrase (which is “I’m wearing my rockin’ Stealth socks!”), and anyone could verify that this phrase produces the above SHA-1 hash. In this way, the above hash proves that I knew the secret phrase without divulging it until I’m ready.

 

 

The cryptographic term for publishing a hash specific to some information is a “commitment”. In this latter example, by publishing the hash, I committed to the phrase “I’m wearing my rockin’ Stealth socks!”. The concept of a commitment is pervasive in cryptographic systems, and especially cryptocurrencies. For example, when users spend cryptocurrencies, they typically sign a commitment to the entire transaction wherein the data from the transaction is hashed (the commitment), and they sign this hash.

Committing to a secret message serves as an important example because it illustrates that hashes are essentially irreversible. It is prohibitively difficult to find a sensible phrase that produces a given SHA-1 hash. Finding two different phrases that produce the same hash is called a “collision”. SHA-1 may not be the best example of a cryptographic hash, because it has been shown to be slightly vulnerable to collisions. Other hash algorithms like SHA256d (used for Bitcoin’s proof-of-work mining) are still considered much more collision resistant and cryptographically secure. Nowadays, SHA-1 is relegated to special use cases, like the derivation of cryptocurrency addresses.

A proof-of-work problem starts with some information and modifies that information to produce hashes that satisfy certain criteria. For example, let’s imagine we want to modify “Stealth rocks!” in such a way that the first character of the SHA-1 hash is 0. In proof-of-work, modification takes the form of simply adding a number to the end of the data, and then hashing the modified data. For example, we can start with the number 1, and add that to the end of “Stealth rocks!” to yield “Stealth rocks!-1”. Note for clarity I also added a hyphen, but it doesn’t change the nature of proof-of-work. The SHA-1 hash of “Stealth rocks!-1” is:

6a02f7befba0af1e4646d651122dcc331cbade68

This hash starts with a 6, so doesn’t meet our criterion of beginning with a “0”. To find the number that works, we can try numbers successively. The first number that produces an SHA-1 hash that satisfies the criterion is 15, meaning the phrase is “Stealth rocks!-15”. The hash is:

044a354080874d578d2de23350f310bb1c8c44cb

This example is a simple proof-of-work. Because there are 16 possible starting characters (“0” through “9” and “a” through “f”), it will take, on average, 16 tries to find a suffix that satisfies the criterion. Although it takes an average of 16 executions of the SHA-1 hash function to find a satisfactory suffix, it only takes one execution of the SHA-1 hash function to validate the result. In other words, a validator only needs to hash the phrase “Stealth rocks!-15” to know that the worker found a satisfactory suffix (“15”).

The number added to the end of the phrase is called a “nonce”. So in this example the nonce “15” gave a hash that met the criterion of starting with a “0”. In a proof-of-work, the nonce is often also called the “work” because it took work to find a satisfactory nonce. The nonce is also often called the “proof”, in that it proves work was done. The convention in the Stealth community is to call the nonce “work” and the output (coupon) that contains the “feework output”. The effort to find the nonce is termed “feework”. As we will see, the feework output includes information in addition to the nonce.

In this example, requiring at least one “0” at the beginning of the hash result is equivalent to requiring that the hash is less than the hexadecimal number 0x10000000000000000000, if the hash string is interpreted as a hexadecimal number itself. This hexadecimal number is equal to the dernary (base ten) number 75,557,863,725,914,323,419,136. Dernary is the number system everyone is exposed to when they first learn how to write their numbers 1 through 10.

All proof-of-work schemes function in basically the same way: the data is modified so that the hash is either less than a cutoff or greater than a cutoff. For Bitcoin proof-of-work and Stealth feework, hashes must be less than a cutoff (called a “ceiling”). For Nano feework, they must be greater than a cutoff (called a “floor”). Practically speaking, there is no difference between requiring the hash to be greater than a floor or less than a ceiling.

The Stealth team chose to require a satisfactory feework hash to be less than a ceiling for aesthetic reasons. A valid Stealth feework hash must be less than the hexadecimal number 0x0006ffffffffffff, which is 1,970,324,836,974,591 dernary. Stealth feework hashes are created by a specialized implementation of the hash function called Argon2d, which returns hashes 8 bytes in length. Eight bytes is 16 characters when expressed in hexadecimal, ignoring the leading “0x” that marks the number as hexadecimal. If expressing a Stealth feework as a 16 character hexadecimal string, it is easy to see the relative work that went into hash simply by counting the zeros at the beginning. I’m somewhat convinced that this is the aesthetic consideration given by the original Bitcoin developers when they invented the Bitcoin proof-of-work mining protocol.

— — — — — — —

 

Stealth Spam Fighting Examples

An important consideration in any proof-of-work scheme is what I call the “validator’s advantage”. In the example above, I noted that a validator only needed to execute the SHA-1 hash function once, even though a worker must execute the SHA-1 hash function 16 times on average. For this example, the validator’s advantage is 16. A first approximation of this advantage can easily be calculated by counting the required leading zeros in a cutoff (if using a ceiling cutoff), then taking 16 to this power. For example, the ceiling cutoff for Stealth feework has three leading zeros, so the validator’s advantage is approximately 16**3 = 4096, where the notation “**” indicates exponentiation (raising to the power).

More accurately, the validator’s advantage is calculated by dividing the ceiling plus one by the maximum possible value of the hash function plus one. The ceiling for Stealth’s feework is 1,970,324,836,974,591, so the denominator is 1,970,324,836,974,592. In hexadecimal, this number looks like 0x0007000000000000. The maximum hash value is 0xffffffffffffffff in hexadecimal, or 18,446,744,073,709,551,615 in dernary. So the numerator is 18,446,744,073,709,551,616. The numerator divided by the denominator is just over 9,362, meaning the validator’s advantage is about 9,362 for Stealth feeless transactions.

 

 

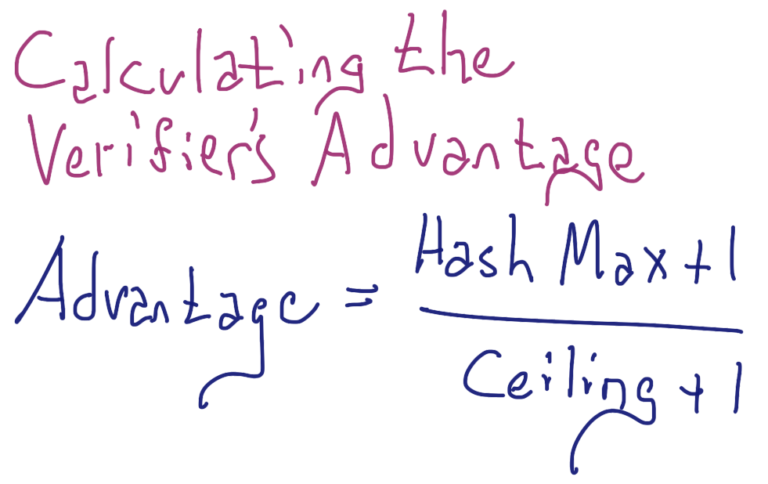
In case the reader is curious, the addition of 1 in both the numerator and denominator reflects the possibility of 0 being a value for a random number between 0 and the hash maximum.

Stealth’s validator’s advantage also describes the average number of times Stealth’s feework hash function needs to be executed to find a valid feework. My desktop, which has average performance per core for new computers, can calculate a typical Stealth feeless hash in about 122 µs (microseconds). Using a single core, it can calculate 9,362 such hashes in just over 1 second. Indeed, Stealth’s feeless ceiling (0x0006ffffffffffff) was chosen so that an average desktop could calculate feework in about 1 second with a single core, which is a reasonable tradeoff for paying a transaction fee.

For a feeless blockchain, the validator’s advantage suggests a maximum transactional throughput. If a single core can calculate 9,362 feeless hashes per second, then that core can verify at most 9,362 feeless transactions per second (tps). This number of transactions is actually quite high. For example bitcoin has averaged about 3 tps over December of 2021. Ethereum averaged about 15 tps over this same period. Visa averages about 1,700 tps, which is less than twice this throughput limit.

Currently, the Stealth blockchain has a “hard coded” block size of 1 MB. Since the target block interval is 5 seconds, Stealth has a data throughput maximum of 0.2 MB per second (MBps). The smallest feeless transaction is 218 bytes, so Stealth has a maximum feeless transactional throughput of about 917 tps, well below the limit imposed by the validator’s advantage (9,362 tps).

Since Stealth is a high performance blockchain, it might gain widespread adoption. At some point in the future, Stealth’s data throughput maximum could be too limiting. In this case, it is straightforward to allow validators to collectively set the block size maximum through a voting mechanism. The infrastructure for deciding blockchain parameters is already in place in the form of StealthNode extensible attributes. Extensible attributes are discussed in detail in our development blog SDBS #21, so I won’t elaborate on them here.

If Stealth’s block size is increased such that the data throughput permits over 9,362 tps, how will validators be able to keep up with the burden of feeless transactions? The answer is that feeless verification can use parallel processing. In other words, a validator can use several CPU cores to verify many feeless transactions concurrently, multiplying the transactional limit approximately by the number of cores available. For example, a 16 core CPU could verify nearly 150,000 feeless transactions per second. Compare this to the Visa network, which carries about 1,700 transactions per second. Clearly, the idea of a blockchain’s requiring 150,000 tps is farfetched, but this analysis shows that the bottleneck won’t be the verification of feeless transactions.

The ability for validators to verify feeless transactions in parallel arises from the requirement that a feeless transaction’s predecessors (input transactions) are confirmed in the blockchain. In other words, there is no need for a validator to check a predecessor before checking a given feeless transaction.

— — — — — — —

 

Feework Structure and its Relation to Fighting Spam

The feework output that serves as a coupon for feeless transactions not only contains (1) a proof-of-work in the form of a 16 byte number, but also (2) a reference block height as a 4 byte number, and (3) the hardness of the hash function as a 4 byte number. Additionally, and less importantly, the coupon has a couple of bytes marking the beginning and end of the output. The layout (data structure) of a feework output is depicted in the following figure:

 

 

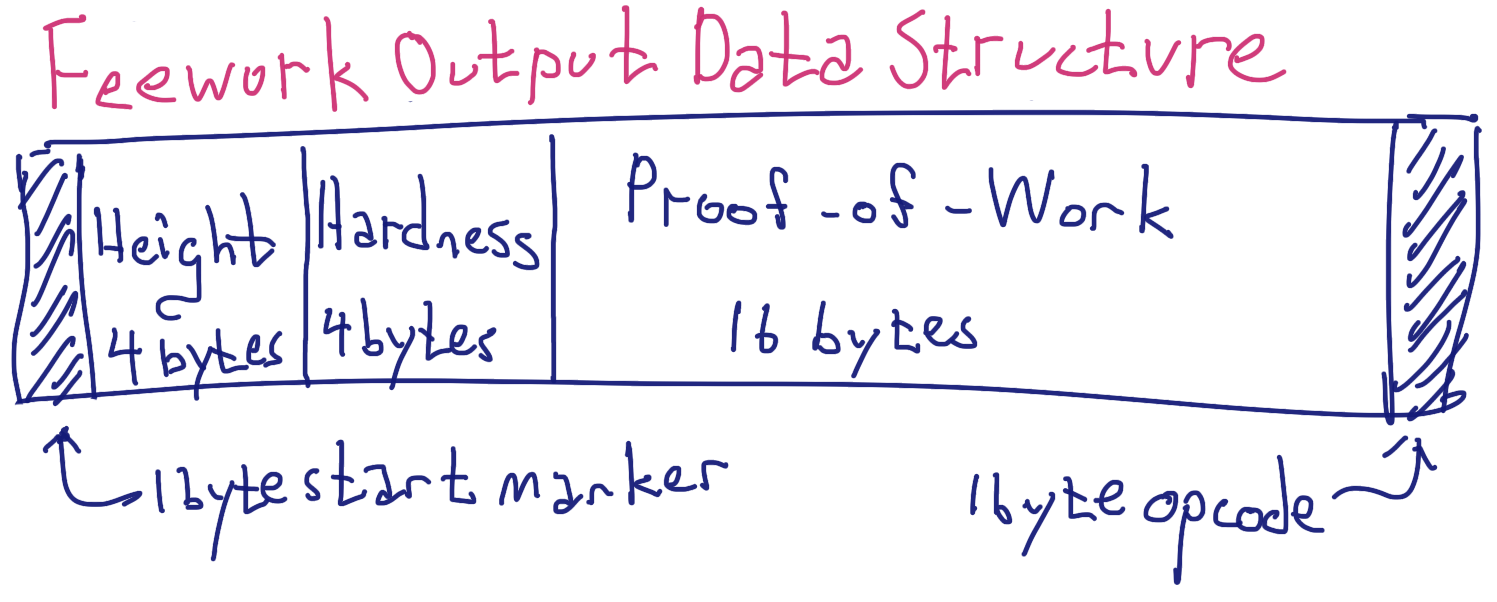
Height, hardness, and the proof-of-work all contribute to fighting spam and are all used, with the rest of the transaction details, to create the data fed to the Stealth feework hash function. As mentioned above, the feework itself is omitted from the transaction data. In the following figure, this omission is represented as cyan shading.

 

 

— — — — — — —

 

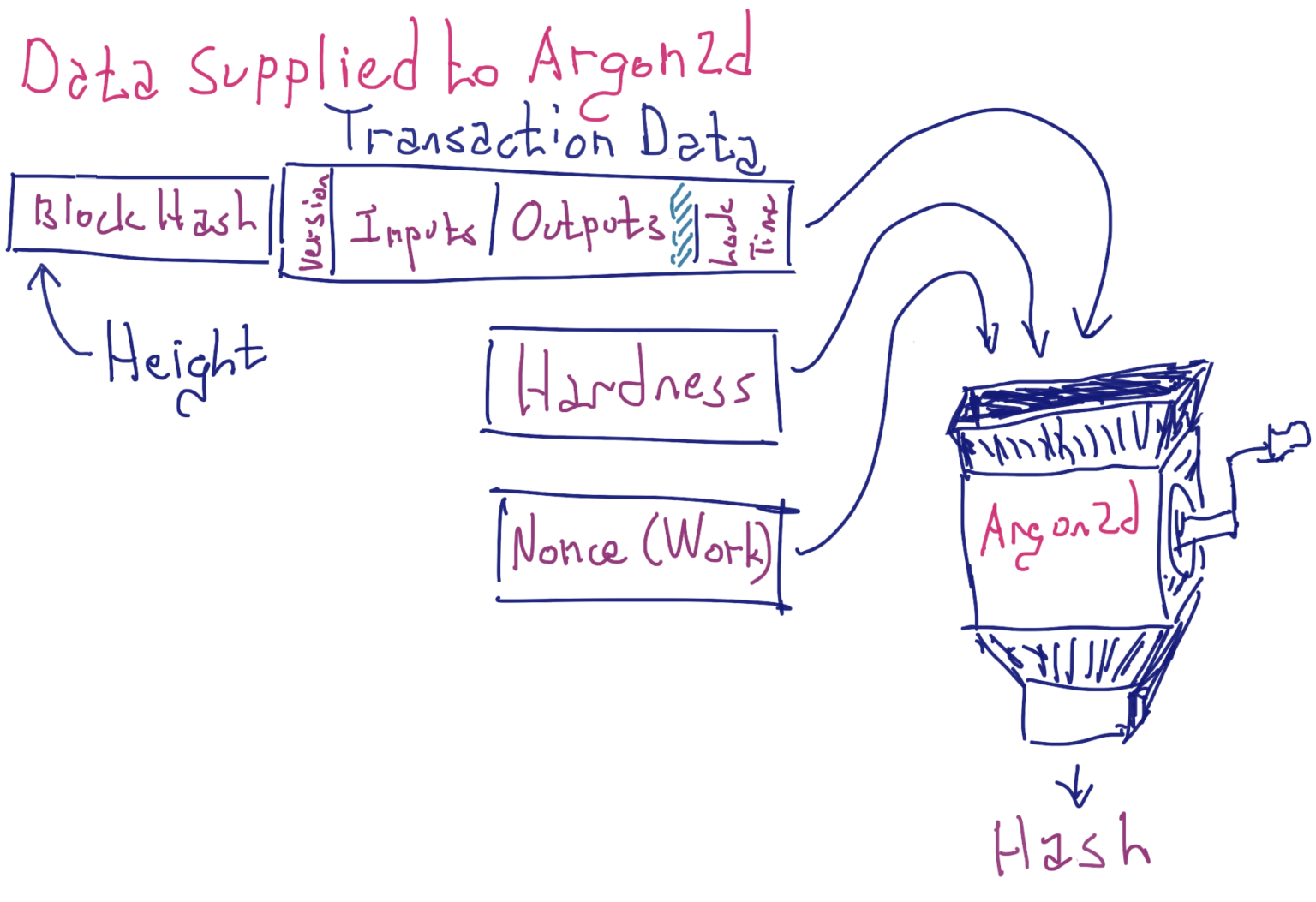
Transaction Details Prevent Reuse of Feework

Including the transaction details in the data supplied to the feework hash commits to a specific transaction, preventing a single feework from being reused for different transactions. The consequence is that an adversary must find a different feework for every spam transaction.

One question is whether an adversary could use phony transactional data, or even simply make up a phony nonce, to trick validators into calculating useless Argon2d hashes. The weakness of this attack is that network nodes that submit bad feework will get banned, and the invalid transactions dropped by the first recipients, without any further transmission. It then becomes a tough game for the adversary to constantly get new network addresses and establish connections, slowing this type of attack to a benign crawl.

— — — — — — —

 

Height Expires the Feework after Two Minutes

The feeless transaction specifies the height of a recent block (typically the most recent). The sender’s wallet determines the main chain hash of the block at this height and prepends this hash to the transaction data. This transaction data does not include the feework, of course, because it is not yet known. To put it succinctly, feework can not work on itself.

Since the hash identifies a specific block, the feework commits to a specific chain, limiting any single feeless transaction to a specific chain. This limitation can reduce the effects of attempted resource exhaustion attacks, where overwhelmed nodes may fork off the main chain.

More importantly, committing to a specific block allows for expiration of the feeless transaction. Stealth feeless transactions expire after 24 blocks (2 minutes), meaning that if a feeless transaction does not make it into a block within 2 minutes, it becomes invalid.

Expiration of feeless transactions have a number of benefits. First, it makes memory pool (mempool) attacks much more difficult. A mempool attack is a type of resource exhaustion attack. The mempool occupies part of the Stealth client’s RAM, storing transactions that have yet to be included in blocks.

One possible attack is to fill the mempool with transactions faster than they can be accepted into blocks. Currently, Stealth’s bandwidth is 917 tps for feeless transactions, so a spammer could begin to flood the mempool with say 1017 tps (100 extra transactions per second). Over time, these excess transactions might build up and overrun (flood) the mempool if transactions never expire.

A low-end virtual private server (VPS) that costs about $15/month can easily allocate 1 GB to the mempool, which corresponds to about 4,000,000 feeless transactions. At 100 extra tps, the mempool would become flooded after about 40,000 seconds, or about 11 hours. At that point, the spammer would only need to spam with 917 tps to keep the mempool flooded. It is worth mentioning again that this attack is contingent on the inability to expire transactions.

However, Stealth feeless transactions expire as fast as they are created (but with a two minute maximum lifespan). Given a 4,000,000 transaction mempool capacity, a spammer would need to spam continuously with over 4,000,000 tps to sustain flooded mempools. Compare this number to the 917 tps needed to sustain a flooded mempool if transactions don’t expire. Clearly, flooding the mempool with feeless transactions will be prohibitive for just about any actor. Even if it only costs $0.00001 to create a feeless transaction, an attacker would need to spend about $144,000 per hour, or about $3.45M per day to keep the mempool flooded, with only a temporary effect on the Stealth network.

— — — — — — —

 

Stealth Feeless Transactions use Memory Hardness

The Stealth feeless transaction protocol incorporates a concept known as memory hardness, which indicates how much memory it will take to produce a specific Argon2d hash. The Argon2d hash function allows for variation in memory hardness, and the Stealth feeless protocol utilizes this potential for variation to prioritize blockchain storage. As blocks become filled up, the hardness requirement increases.

Stealth is the only cryptocurrency that uses a memory-hard hashing algorithm for spam prevention. But, we are certain memory hardness will one day become the standard for feeless transactions.

A feeless transaction that gets into an empty Stealth block must have feework that requires at least 262 kilobytes (KB) of memory to produce. For a feeless transaction to be accepted into a Stealth block that is nearly 20% full, its feework must require at least 819 KB.

Imagine a bad actor who wants to spam the Stealth network with graphical processing units (GPUs) in a denial of service (DoS) attack. How many GPUs would this bad actor need to fill blocks to 20% with feeless transactions?

An excellent GPU for mining Argon2d is the Tesla V100, which costs about $7,000 new and has 12 GB of RAM. Based on online benchmarks, a single Tesla V100 should manage about 360,000 hashes per second (Hps) under these conditions wherein blocks are 20% full. Such a GPU could mine about 88 feeless transactions per second. Stealth has a 917 tps feeless throughput, so it would take just over two such GPUs to fill blocks with 20% feeless transactions, if these GPUs had no competition from legitimate users.

Currently, the Stealth protocol will permit feeless transactions to occupy at most 20% of any block. Thus, even if an adversary ran over $14,000 of graphics cards at maximum capacity, legitimate users could simply pay inexpensive fees (about $0.00025 each) until the spammer got tired of wasting energy, with barely any impact on the user experience.

Another option for users would be to simply specify a higher memory hardness when they create a feeless transaction. For inclusion in a given block, a transaction with a higher memory hardness will always take priority over a transaction with lower memory hardness. For the maximum hardness permitted by the Stealth protocol, a user would need to wait about 14 seconds on average to produce a valid feework on a typical desktop computer.

Fourteen seconds is admittedly a long time to wait for a computer to generate feework, creating a minor inconvenience for users. However, the higher memory hardness translates into significant adversity for a spammer. The maximum hardness corresponds to an 18 fold increase in memory requirements. While the time dependence on memory hardness for CPUs (legitimate users) is slightly sublinear, it is superlinear for GPUs, and the number of GPUs required to crowd out legitimate feeless users would jump to an estimated 40, or $280,000 of equipment. Even with this investment by an adversary, users could simply pay the small fee (about $0.00025 at the time of writing), negating the whole attack.

Could a well funded adversary create a surprise attack on the Stealth network and “freeze” user transactions that have not yet gotten into blocks, thereby freezing some of their funds? Imagine that users are happily and legitimately using feeless transactions, submitting their feework with close to the minimum memory hardness. An adversary decides that he will run $280,000 of GPUs indefinitely to freeze all the low-hardness transactions such that these transactions will not get into blocks. Within seconds, all legitimate, low hardness transactions would be crowded out by the spammer. Unfortunately for the spammer, this attack would inconvenience legitimate users for at most 2 minutes. After that, the legitimate transactions would expire, the users would get their funds back, and could re-submit transactions with a small fee in XST, again negating the attack.

— — — — — — —

 

Stealth: A Powerful Approach to Fighting Spam

I hope this little writeup made a convincing case for the Stealth feeless protocol, which was designed to thwart any conceivable exploit that may arise when offering feeless transactions. Other blockchains, like Nano, have spam prevention, but their specific implementations and protocol designs result in compromises not needed by Stealth.

Fast. Secure. Reliable.

Get the Stealthsend Desktop App

What is Stealth

Junaeth

FAQs

Whitepaper

StealthMonitor

Apps

Roadmap

News / Blog

Github Source

Privacy Policy

Terms of Use

Cookie Policy